ILMU UKUR TANAH
Pengertian ilmu ukur tanah adalah, Ilmu yang mempelajari Tentang bumi, yaitu memindahkan Atau menggambarkan Permukaan Bumi, baik di darat, di laut, melalui pengukuran udara ke dalam peta yang memiliki skala Peta.
Skala peta adalah Perbandingan antar 2 Objek, Objek nyata (yang kita ukur dan Objek hasil yang kita gambar) perbandingan tersebut didapat setelah kita melakukan pengukuran,
Di Bangku perkuliahan Teknik Sipil, Ilmu Ukur tanah di pelajari pada semester awal, di sana mempelajari tentang bagaimana penggunaan alat survei Theodolite dan Waterpass Level, dan di hitung menggunakan Rumus dasar ilmu ukur tanah, Sedangkan di Perkuliahan Geodesi, lebih mendetail sampai dengan analisa dalam arti cakupan luas
yang di pelajari yaitu cara menghitung koreksi sudut vertikal dan horizontal, sudut tersebut diantaranya kesalahan penutup sudut, kesalahan orang itu sendiri, kesalahan kolimasi supaya menghasilkan perhitungan yang masuk toleransi, di bangku kuliah teknik sipil juga menghitung sudut,
Contohnya:
- Sudut jurusan, Koordinat titik
- Trigonometri
- Menentukan sudut jurusan dan jarak
- Menghitung Azimuth
Sudut Jurusan adalah : Sudut yang dihitung mulai dari sumbu Y+ (arah utara) berputar searah jarum jam sampai titik yang di tuju, Sudut Jurusan mempunyai nilai: 0 derajat sampai dengan 360 derajat dan dua sudut yang berlawanan berselisih, untuk gambarannya saya sisipkan di bawah ini:
 |
| Gambar 001- Tembakan ke Belakang (Backsight) |
 |
| Gambar 002 - Tembakan Ke Depan (Forsight) |
 |
| Gambar 003- Kembali dalam keadaaan 180 derajat |
dari gambaran di atas 001 S/D 003, sudut jurusan secara aplikasi adalah sebuah formasi membentuk segitiga, ketika pengukuran di lapangan dilaksanakan, anda harus mempunyai referensi awal, referensi bisa menggunakan koordinat lokal dan global (Nanti kita bahas), saat penembakan ke belakang, dan ke depan itu harus dalam waktu yang singkat, untuk meminimalisir kesalahan.
Jadi sudut Jurusan memiliki Rumus:
α ba = α ab + 180° atau α ba - α ab = 180°
Koordinat titik:
Untuk menentukan titik-titik yang tidak terletak pada satu garis lurus, maka cara yang kita gunakan yaitu melalui pertolongan dua buah garis lurus yang saling tegak lurus, yang biasa disebut sumbu.
 |
| Gambar 004 Garis Sumbu (salib Sumbu) |
Garis yang mendatar dinamakan absis atau sumbu X, sedangkan garis yang vertikal dinamakan ordinat atau sumbu Y.
Di dalam Ilmu Ukur Tanah digunakan Peraturan sebagai berikut :
- Sumbu Y positif dihitung ke arah utara
- Sumbu X positif dihitung ke arah timur
- Kuadran 1 terletak antara Y+ dan X+
- Kuadran 2 terletak antara Y- dan X+
- Kuadran 3 terletak antara Y- dan X-
- Kuadran 4 terletak antara Y+ dan X-
Trigonometri:
 |
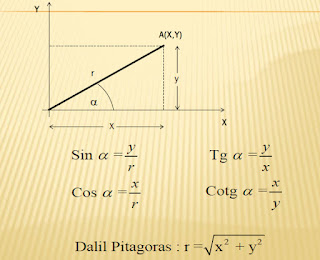| 005 - Gambar Pitagoras |
Berikut Rumus Trigonometri, di mana mempunyai Rumus dan dalil Pitagoras
Menentukan Sudut dan Jarak:
Apabila diketahui Koordinat Titik A (Xa, Ya) dan B (Xb, Yb),
 |
| Gambar 006 |
dan dari Rumus Pitagoras diperoleh :
 |
| Gambar 007 |
Menghitung Azimut:
Di dalam peta setiap titik letaknya dihitung dari dua salib sumbu yang saling tegak lurus, yang horisontal di-sebut sumbu X dan yang tegak disebut sumbu Y.
Perpotongan dari dua salib sumbu itu diberi angka 0 Sumbu X, yang ada di sebelah kanan sumbu tegak diberi tanda positif (+) dan yang di sebelah kiri diberi tanda negatif (-).
Sedangkan sumbu Y yang di sebelah atas sumbu X diberi tanda positif (+) dan sumbu Y ada di sebelah bawah sumbu X diberi tanda negatif (-).
 |
| Gambar 008 |
Kedudukan azimuth garis pada kwadran
α = Kedudukan sudut yang dibentuk oleh sumbu Y dan garis bidik A → B
Pada Gambar 008 , memperlihatkan kedudukan azimuth garis A → B pada masing-masing kwadran. Untuk menghitung azimuth garis pada masing-masing kwadran berlaku persamaan sebagai berikut:
tg α A → B = (XB – XA)/(YB – YA)
α A → B = Azimut garis A → B
XA, YA = Koordinat titik A
XB, YB = Koordinat titik B
 |
| Gambar 009 Pada gambar 009 di perlihatkan posisi - posisi dari kuadran secara mendetail di mana: Pada kwadran I : α = α AB; Pada kwadran II : α AB = 180°+ α; Pada kwadran III : α AB = 180°+ α Pada kwadran IV : α AB = 360°+ α |
CONTOH 1:
Diketahui koordinat titik:
A : XA = 1000 m; YA = 1000 m
B : XB = 2000 m; YB = 2000 m
Ditanyakan Azimut A → B (α AB) Penyelesaian:
dx = XB – XA = 2000 – 1000 = 1000 m
dy = YB – YA = 2000 – 1000 = 1000 m
tg α A → B = dx/dy = 1000/1000 = +1
dx = + dan dy = +
maka arah jurusan garis A → B ada di kwadran I
α = 45°
AB = α; = 45°
 |
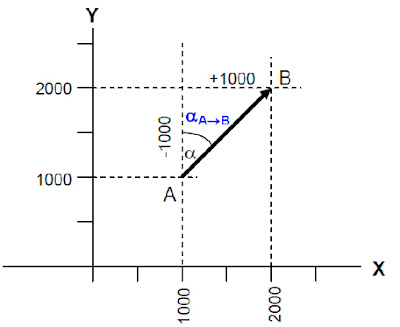| Gambar 010 - Kedudukan garis A → B pada kwadran I |
α = sudut hasil perhitungan
α AB = Azimut garis A → B
B α = α A → B
Bagaimana sudah ada masukan ke Logikanya, sudah mencobanya? jika belum saya kasih tambahan, dan harus mencoba 2 soal ini:
Contoh 2:
Diketahui koordinat titik: A : XA = 1000
m; YA = -1000 m B : XB = 2000 m; YB = -2000 m
Ditanyakan jarak A → B (j A → B)
Penyelesaian
dx = XB – XA = 2000 – 1000 = 1000 m
dy = YB – YA = -2000 – (-1000) = -1000 m
tg α A → B = dx/dy = 1000/-1000 = -1
dx = + dan dy = - maka arah jurusan garis A → B ada di kwadran II
α = - 45°, α A → B = 180° + α = 180 ° + (-45°) = 135°
1). J = dx/sin α A pnh B = 1000/sin135° = 1414,213562 m
2). J = dy/cos α A pnh B = -1000/cos135 ° = 1414,213562 m
3). J = ((XB – XA) + (YB – YA)² )1/2(setengah kwadrat)
= ((2000 – 1000) + (-2000 – (- 1000)² )1/2(setengah kwadrat)
= 1414,213562 m
Nah setelah kita bahas secara singkat mengenai pengertian, Rumus dan Contoh perhitungan, sekarang silakan mengerjakan soal latihan di bawah ini:
Latihan 1
Diketahui koordinat titik: A : XA = -1000 m; YA = -1000 m
B : XB = -2000 m; YB = -2000 m
Ditanyakan jarak A → B
Latihan 2
Diketahui koordinat titik: A : XA = -1000 m; YA = +1000 m
B : XB = -2000 m; YB = +2000 m
Ditanyakan jarak A → B
Menghitung koordinat titik Koordinat suatu titik dapat dihitung apabila titik tersebut:
1. Diikatkan pada suatu titik yang diketahui koordinatnya
2. Jarak antara dua titik diukur
3. Azimut antara dua titik diketahui
lihat gambar di bawah ini:
 |
| Gambar 011 |
Dari gambar 011 dapat di simpulkan:
Keterangan:
→ = Jarak garis A ke B yang diukur
α A → B = Azimut garis A → B
A = Titik yang telah diketahui koordinatnya
B = Titik yang dihitung koordinatnya
Untuk menghitung koordinat titik B terhadap titik A, persamaannya adalah:
XB = XA + jA → B x sin α A → B
YB = YA + jA → B x cos α A → B
KESIMPULAN:
Dari pembahasan yang kami rangkum dalam sebuah artikel, mengingatkan kita pentingnya kajian-kajian khusus di mana rumus adalah sumber segalanya, untuk menjawab baik perhitungan matematika, dan dalam kehidupan seperti halnya hidup, tanpa ilmu kita tidak akan menjadi daun, karena daun melalui proses fotosintesis,, bukan hasil yang di dapat melainkan proses hasil yang akan mendapatkan,
Begitu juga dengan halnya di atas, dalam pembahasan sederhana mengingatkan akan pentingnya dasar ilmu atau disiplin ilmu dasar, karena tanpa dasar kita tidak akan meraih tengah atau atas dari situlah rumus hidup sama halnya dalam ilmu ukur tanah memiliki rumus, fungsi dan pertanyaan yang harus di Jawab.....
Intinya dalam pembahasan kali ini:
Pelajari kwadran, karena dasar pekerjaan pengukuran untuk menentukan sudut bangunan yang tidak di ketahui asal usul desainnya (Atau yang tersedia hanya hamparan area yang luas) tidak mempunyai referensi sedikitpun, itu dapat di jawab dengan sistem lokal koordinat, menggunakan kompas dan lain-lain.
bangunan konstruksi, ketika staking out jika hafal kwadran maka kita akan memprediksi posisi titik yang akan kita cari, berdasarkan arah utara sebenarnya dan peta, itu dapat di pakai dalam pekerjaan konstuksi bangunan tinggi, jembatan, pekerjaan irigasi, jalur pipa pertamina, dan sebagainya,
Perhitungan koordinat yang di ketahui dan tidak diketahui, ini dapat dihitung dengan rumus di atas,
dan kita akan bahas dalam perhitungan table koordinat.
Artikel Lain:
Tidak ada komentar:
Posting Komentar